6 Mathematical background

6.1 Decay models

PyFDAP supports two different decay models: Linear- and non-linear decay. Linear decay is given by the ordinary differential equation (ODE)

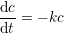dc- dt = - kc

where c is the concentration of a molecule and k is the rate constant of the decay. Since we assume that the level of fluorescence is proportional to the molecule concentration, we can substitute the concentration with fluorescence intensity. Solving this ODE results in

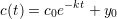c(t) = c0e- kt + y0

where c(t) is the concentration of a molecule at time t, c(0) = c₀ is the concentration at time t = 0, and y₀ is the baseline fluorescence intensity to which the population of decaying molecules converges. In terms of fluorescence intensity, y₀ resembles the baseline level of noise and autofluorescence. From k we can then compute the molecule’s half-life τ by

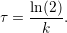τ = ln(2). k

Some molecules are proposed to decay non-linearly (Eldar et al., 2003), and we have

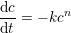dc ---= - kcn dt

where n > 1 is the degree of non-linearity and k is the decay rate constant of the molecule. We can solve this ODE and obtain the power-law solution

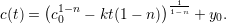( 1-n )11-n c(t) = c0 - kt(1 - n) + y0.

For the case of a non-linear decay model, we compute the molecule’s half-life by

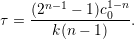(2n- 1 - 1)c1-n τ = ----------0--. k(n- 1)

6.2 Estimation of initial guesses and bounds for variables

PyFDAP offers multiple options to calculate initial guesses and bounds for variables that are used by the fitting algorithms to obtain biologically reasonable estimates based on noise, pre-conversion, and background measurements (see Section 4).

Initial guess for the estimation of c₀: A good estimate for c₀ is the difference between the pre-conversion and the first post-conversion image, i.e.

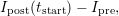Ipost(tstart) - Ipre,

where I_post and I_pre are the fluorescence intensities after and before photoconversion, respectively, and t_start is the time at which the first image was taken.

Initial guess for the estimation of the baseline y₀: PyFDAP offers the two presets I_post(t_start) and I_post(t_end), where t_end is the time at which the last image was taken and where protein decay should be almost complete. Our tests showed that the optimization algorithms worked well if y_0,opt is approached from above using I_post(t_start) as the initial guess for y₀.

Estimation of the lower bound for the baseline y₀: This estimate is a crucial part of the fitting process. PyFDAP offers several algorithms to perform this estimation based on the amount and quality of the data available.

The simplest estimate of the lower bound of y₀ is the average background noise of the measurements N. Due to autofluorescence of the samples, this estimate is generally too low, but it serves as the lower bound of the lower bounds of y₀.
Alternatively, the lower bound of the baseline y₀ can be estimated from the average level of autofluorescence represented by
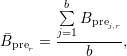
$∑b Bprej,r B¯ = j=1-------, prer b$

where r ∈{intracellular, extracellular, entiredomain} is the investigated region, and j ∈{1,...,b} are the indices of background pre-conversion datasets with intensities B_{pre_j,r}.
PyFDAP also offers the possibility to use the average background intensity as the lower bound of the baseline y₀:
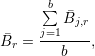
$∑b ¯Bj,r B¯r = j=1-----, b$

where B_j,r is the mean intensity in region r of a background dataset over all data points given by
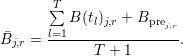
$∑T B(tl)j,r + Bprej,r B¯j,r = l=1----------------. T + 1$

Here, t_l with l ∈{1,...,T} is the time when the l-th image was taken and T is the number of post-conversion images.
PyFDAP includes a special weighting function F (Müller et al., 2012) given by
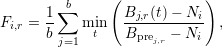
$b ( ) F = 1∑ min Bj,r(t)---Ni , i,r bj=1 t Bprej,r - Ni$

where i is the current FDAP measurement, r is the investigated region, and j is the index of background datasets with intensities B(t) at time t. Here, the noise measurement of measurement i is given by N_i. Using the function F, users can compute the lower bound of the baseline y_{0_i,r} for measurement i and region r by
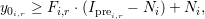
$y ≥ F ⋅(I - N ) + N , 0i,r i,r prei,r i i$

where I_{pre_i,r} denotes the pre-conversion intensity of the FDAP measurement i in region r.

6.3 Optimization algorithms

PyFDAP comes with a wide selection of optimization algorithms taken from the SciPy optimize package (http://docs.scipy.org/doc/scipy/reference/optimize.html) (Nelder and Mead (1965); Polak and Ribière (1969); Broyden (1970); Goldfarb (1970); Fletcher (1970); Shanno (1970); Nash (1984); Kraft (1988); Byrd et al. (1995); Nocedal and Wright (2006)). A list of all optimization algorithms available in PyFDAP can be found in Table 3.

Bounded methods

Unbounded methods

Method	Name in PyFDAP	Type	Reference



Limited-memory BFGS	L-BFGS-B	quasi-Newton	Byrd et al. (1995)

Truncated Newton Conjugate	TNC	Newton conjugate	Nash (1984)

Sequential Least Squares Programming	SLSQP	sequential quadratic	Kraft (1988)

Brute force	brute	brute force	SciPy Reference Guide



Nelder-Mead	Nelder-Mead	simplex	Nelder and Mead (1965)

Broyden-Fletcher-Goldfarb-Shanno	BFGS	quasi-Newton	Broyden (1970); Goldfarb (1970); Fletcher (1970); Shanno (1970)

Nonlinear Conjugate Gradient	CG	Newton conjugate	Polak and Ribière (1969)

Table 3: List of optimization algorithms in PyFDAP.

6.4 Statistics

PyFDAP can average over multiple fits from different embryo objects (FDAP measurements). Details of how to select fits for averaging are described in Section 3.3.

PyFDAP averages the optimal parameters for k, y₀, c₀, and protein half-lives τ through an arithmetic mean. For example, the average decay rate constant k is obtained by

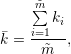m∑˜ ki ¯k = i=1---, m˜

where 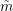is the number of fits to be averaged. The average half-life τ can be computed in two ways resulting in different average half-lives. PyFDAP computes the average half-life τ through the arithmetic mean given by

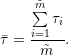∑˜m τi ¯τ = i=1--. m˜

For the linear decay model, this yields

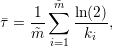˜m 1-∑ ln(2) ¯τ = ˜m ki , i=1

(1)

and in the case of the non-linear decay model we obtain

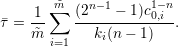1-∑˜m (2n--1 --1)c10-,in τ¯= ˜m ki(n - 1) . i=1

(2)

However, computing the average half-life τ directly from the average decay rate k yields

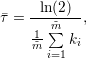¯τ = -ln(2)-, 1-∑˜m ˜m ki i=1

(3)

for the linear decay model and

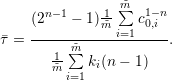m˜ (2n-1 - 1) 1-∑ c1- n ----------˜m-i=1--0,i- ¯τ = 1 m∑˜ . ˜m- ki(n - 1) i=1

(4)

in case of the non-linear decay model. It is obvious that equations 1 and 3 as well as equations 2 and 4 do not produce the same half-lives, and the user needs to decide which way of half-life computation is appropriate for the application.

PyFDAP can produce different error bar plots for each averaged region. Clicking on Statistics → Plotting → Plot average fit will result in a plot in which each average data point c(t_j) is computed as the arithmetic mean

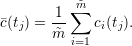∑˜m ¯c(tj) = 1- ci(tj). ˜m i=1

Error bars are computed as the standard deviation for each time t_j. Clicking on Statistics → Plotting → Plot normed average fit returns a plot in which all data points are normalized between values of 0 and 1. The normalization is performed by subtracting the baseline value y_0,i from each data point and dividing the result by c_0,i, i.e.

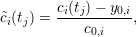ci(tj)- y0,i ˜ci(tj) = ----------, c0,i

where 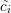c˜i (t_j) is the normalized data point at time t_j. This normalization facilitates the comparison of decay curve shapes, but it substantially changes the meaning of the error bars. Since all data series are pinned to a value of 1 at their first time point, the standard deviation vanishes for this data point. The following data points will generally produce increasing error bars since the decay curves generally diverge. The length of the normalized error bars can be interpreted as the extent to which the decay curves diverge throughout the experiments.